Critical Connections in a Network

There are n servers numbered from 0 to n-1 connected by undirected server-to-server connections forming a network where connections[i] = [a, b] represents a connection between servers a and b. Any server can reach any other server directly or indirectly through the network.

A critical connection is a connection that, if removed, will make some server unable to reach some other server.

Return all critical connections in the network in any order.

Example 1:

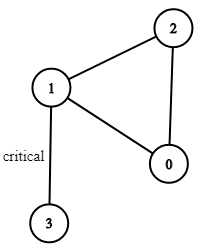
Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
Output: [[1,3]]
Explanation: [[3,1]] is also accepted.

Constraints:

1 <= n <= 10^5
n-1 <= connections.length <= 10^5
connections[i][0] != connections[i][1]
There are no repeated connections.

Solution:

Tarjan’s algo for finding articulation points

class Solution {
public:
    
    
    void art(int u, int& cnt, vector<int>& dfs, vector<int>& low, vector<int>& par, vector<vector<int>>& edge, vector<vector<int>>& ans){
        dfs[u] = cnt++;
        low[u] = dfs[u];
        cout<<u<<" "<<dfs[u];
        
        for(int v : edge[u]){
            if(dfs[v] == -1){
                par[v] = u;
                art(v, cnt, dfs, low ,par, edge, ans);
                low[u] = min(low[u], low[v]);
                if(low[v] > dfs[u]){
                    ans.push_back(vector<int>{u,v});
                }
                    
            }else if(v != par[u]){
                low[u] = min(low[u], dfs[v]);
            }
        }
        
    }
    vector<vector<int>> criticalConnections(int n, vector<vector<int>>& conn) {
        vector<int> dfs(n,-1);
        vector<int> low(n,-1);
        vector<int> par(n,-1);

        int cnt = 0;
        vector<vector<int>> ans;

        vector<vector<int>> edge(n);
        for(int i = 0;i < conn.size(); i++){
            int x = conn[i][0];
            int y = conn[i][1];
            edge[x].push_back(y);
            edge[y].push_back(x);
        }
        art(0, cnt, dfs, low ,par, edge, ans);
        return ans;
        
    }
};